Supervised Learning(Part-5)

 Decision Trees (Continued)



Attribute Selection Measures

If the dataset consists of N attributes then deciding which attribute to place at the root or at different levels of the tree as internal nodes is a complicated step. By just randomly selecting any node to be the root can’t solve the issue. If we follow a random approach, it may give us bad results with low accuracy.

For solving this attribute selection problem, researchers worked and devised some solutions. They suggested using some criteria like :
  1. Entropy,
  2. Information gain,
  3. Gini index,
  4. Gain Ratio,
  5. Reduction in Variance
  6. Chi-Square

These criteria will calculate values for every attribute. The values are sorted, and attributes are placed in the tree by following the order i.e, the attribute with a high value(in case of information gain) is placed at the root.
While using Information Gain as a criterion, we assume attributes to be categorical, and for the Gini index, attributes are assumed to be continuous.


Entropy

Entropy is a measure of the randomness in the information being processed. The higher the entropy, the harder it is to draw any conclusions from that information. Flipping a coin is an example of an action that provides information that is random.



From the above graph, it is quite evident that the entropy H(X) is zero when the probability is either 0 or 1. The Entropy is maximum when the probability is 0.5 because it projects perfect randomness in the data and there is no chance if perfectly determining the outcome.


ID3 follows the rule — A branch with an entropy of zero is a leaf node and A branch with entropy more than zero needs further splitting.

Mathematically Entropy for 1 attribute is represented as:



Where S → Current state, and Pi → Probability of an event i of state S or Percentage of class i in a node of state S.

Mathematically Entropy for multiple attributes is represented as:



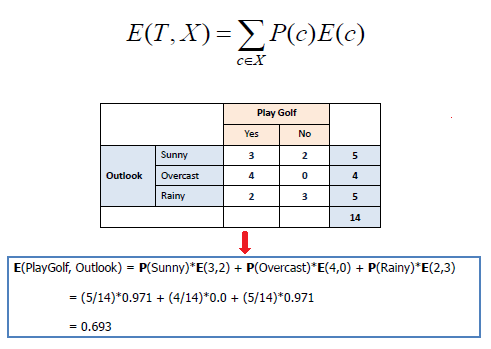
where T→ Current state and X → Selected attribute


Information Gain

Information gain or IG is a statistical property that measures how well a given attribute separates the training examples according to their target classification. Constructing a decision tree is all about finding an attribute that returns the highest information gain and the smallest entropy.




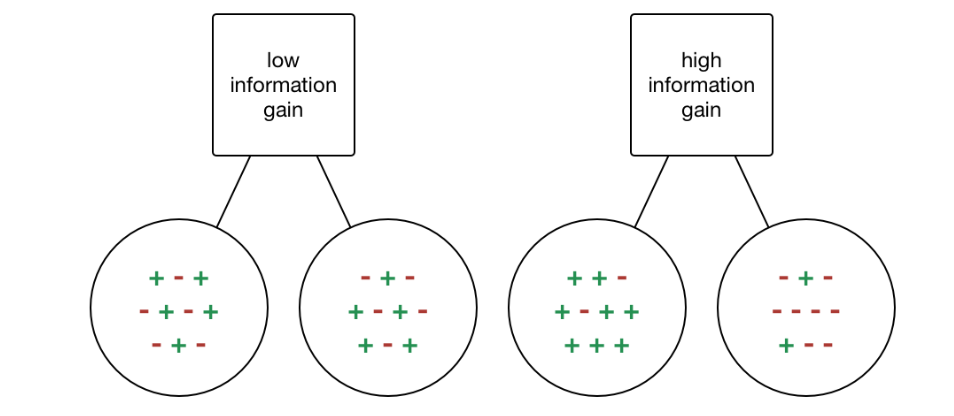
Information gain is a decrease in entropy. It computes the difference between entropy before split and average entropy after split of the dataset based on given attribute values. ID3 (Iterative Dichotomiser) decision tree algorithm uses information gain.

Mathematically, IG is represented as:



In a much simpler way, we can conclude that:



Where “before” is the dataset before the split, K is the number of subsets generated by the split, and (j, after) is subset j after the split.


Gini Index

You can understand the Gini index as a cost function used to evaluate splits in the dataset. It is calculated by subtracting the sum of the squared probabilities of each class from one. It favors larger partitions and easy to implement whereas information gain favors smaller partitions with distinct values.



Gini Index works with the categorical target variable “Success” or “Failure”. It performs only Binary splits.


Higher the value of Gini index higher the homogeneity.

Steps to Calculate Gini index for a split
Calculate Gini for sub-nodes, using the above formula for success(p) and failure(q) (p²+q²).
Calculate the Gini index for split using the weighted Gini score of each node of that split.

CART (Classification and Regression Tree) uses the Gini index method to create split points.


Gain ratio

Information gain is biased towards choosing attributes with a large number of values as root nodes. It means it prefers the attribute with a large number of distinct values.

C4.5, an improvement of ID3, uses Gain ratio which is a modification of Information gain that reduces its bias and is usually the best option. Gain ratio overcomes the problem with information gain by taking into account the number of branches that would result before making the split. It corrects information gain by taking the intrinsic information of a split into account.


Let us consider if we have a dataset that has users and their movie genre preferences based on variables like gender, group of age, rating, blah, blah. With the help of information gain, you split at ‘Gender’ (assuming it has the highest information gain) and now the variables ‘Group of Age’ and ‘Rating’ could be equally important and with the help of gain ratio, it will penalize a variable with more distinct values which will help us decide the split at the next level.


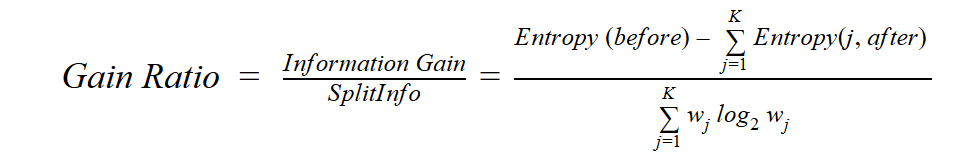
Where “before” is the dataset before the split, K is the number of subsets generated by the split, and (j, after) is subset j after the split.


Reduction in Variance

Reduction in variance is an algorithm used for continuous target variables (regression problems). This algorithm uses the standard formula of variance to choose the best split. The split with lower variance is selected as the criteria to split the population:



Above X-bar is the mean of the values, X is actual and n is the number of values.

Steps to calculate Variance:
Calculate variance for each node.
Calculate variance for each split as the weighted average of each node variance.


Chi-Square

The acronym CHAID stands for Chi-squared Automatic Interaction Detector. It is one of the oldest tree classification methods. It finds out the statistical significance between the differences between sub-nodes and parent node. We measure it by the sum of squares of standardized differences between observed and expected frequencies of the target variable.

It works with the categorical target variable “Success” or “Failure”. It can perform two or more splits. Higher the value of Chi-Square higher the statistical significance of differences between sub-node and Parent node.

It generates a tree called CHAID (Chi-square Automatic Interaction Detector).

Mathematically, Chi-squared is represented as:



Steps to Calculate Chi-square for a split:
Calculate Chi-square for an individual node by calculating the deviation for Success and Failure both
Calculated Chi-square of Split using Sum of all Chi-square of success and Failure of each node of the split


How to avoid/counter Overfitting in Decision Trees?

The common problem with Decision trees, especially having a table full of columns, they fit a lot. Sometimes it looks like the tree memorized the training data set. If there is no limit set on a decision tree, it will give you 100% accuracy on the training data set because in the worse case it will end up making 1 leaf for each observation. Thus this affects the accuracy when predicting samples that are not part of the training set.

Here are two ways to remove overfitting:
Pruning Decision Trees.
Random Forest

Pruning Decision Trees

The splitting process results in fully grown trees until the stopping criteria are reached. But, the fully grown tree is likely to overfit the data, leading to poor accuracy on unseen data.



Pruning in action

In pruning, you trim off the branches of the tree, i.e., remove the decision nodes starting from the leaf node such that the overall accuracy is not disturbed. This is done by segregating the actual training set into two sets: training data set, D and validation data set, V. Prepare the decision tree using the segregated training data set, D. Then continue trimming the tree accordingly to optimize the accuracy of the validation data set, V.




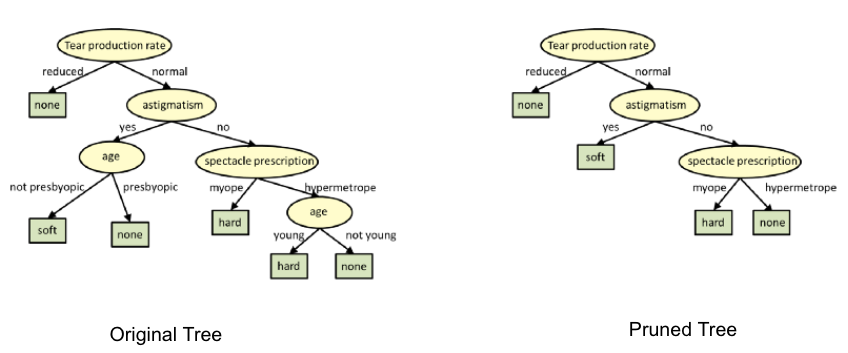
In the above diagram, the ‘Age’ attribute in the left-hand side of the tree has been pruned as it has more importance on the right-hand side of the tree, hence removing overfitting.

Random Forest

Random Forest is an example of ensemble learning, in which we combine multiple machine learning algorithms to obtain better predictive performance.

Why the name “Random”?

Two key concepts that give it the name random:
A random sampling of training data set when building trees.
Random subsets of features considered when splitting nodes.

A technique known as bagging is used to create an ensemble of trees where multiple training sets are generated with replacement.

In the bagging technique, a data set is divided into N samples using randomized sampling. Then, using a single learning algorithm a model is built on all samples. Later, the resultant predictions are combined using voting or averaging in parallel.




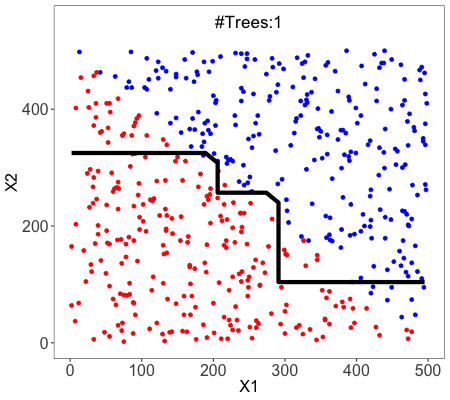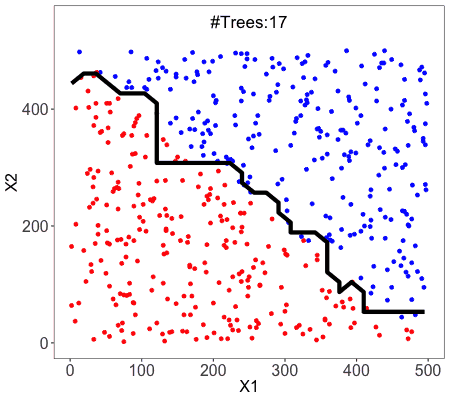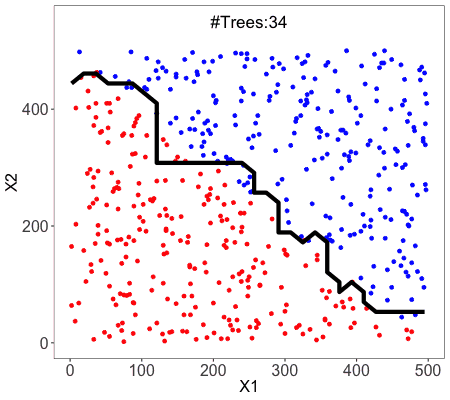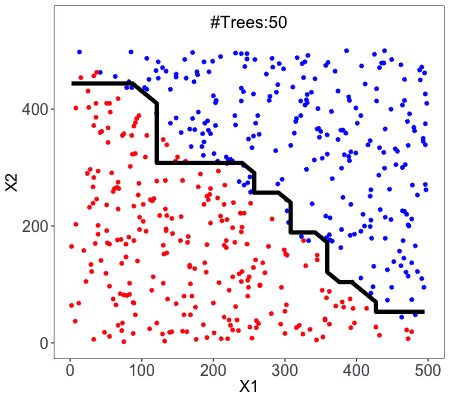
Pros vs Cons of Decision Trees

Advantages:
  1. The main advantage of decision trees is how easy they are to interpret. While other machine Learning models are close to black boxes, decision trees provide a graphical and intuitive way to understand what our algorithm does.
  2. Compared to other Machine Learning algorithms Decision Trees require less data to train.
  3. They can be used for Classification and Regression.
  4. They are simple.
  5. They are tolerant to missing values.
Disadvantages
  1. They are quite prone to over fitting to the training data and can be sensible to outliers.
  2. They are weak learners: a single decision tree normally does not make great predictions, so multiple trees are often combined to make ‘forests’ to give birth to stronger ensemble models. This will be discussed in a further post.

Comments

Post a Comment

Popular posts from this blog

Supervised Learning(Part-2)

Image
  Support Vector Machine A Support Vector Machine (SVM) is a discriminative classifier formally defined by a separating hyperplane. In other words, given labeled training data, the algorithm outputs an optimal hyperplane which categorizes new examples.  In two dimensional space this hyperplane is a line dividing a plane in two parts where in each class lay in either side. Suppose given plot of two label classes on graph as shown in image. You might have come up with something similar to following image (image B). It fairly separates the two classes. Any point that is left of line falls into black circle class and on right falls into blue square   In real world application, finding perfect class for millions of training data set takes lot of time. This is called regularization parameter.  Two terms regularization parameter and gamma are tuning parameters in SVM classifier. Varying those we can achieve considerable non linear classification line with more accuracy in reasonable amount of
Read more

Convolutional Neural Networks(Part-2)

Image
  Cross- Correlation Cross-correlation  is a  measure of similarity  of two series as a function of the displacement of one relative to the other. This is also known as a  sliding  dot product  or  sliding inner-product . It is commonly used for searching a long signal for a shorter, known feature. It has applications in  pattern recognition ,  single particle analysis ,  electron tomography ,  averaging ,  cryptanalysis , and  neurophysiology .  Steps followed in Cross- Correlation Take two matrices with same dimensions. Multiply them one by one, element by element (i.e , not the dot product, just the simple multiplication). Sum the elements together. VGG16 VGG16 is a convolutional neural network model proposed by K. Simonyan and A. Zisserman from the University of Oxford in the paper “Very Deep Convolutional Networks for Large-Scale Image Recognition”.  The model achieves 92.7% top-5 test accuracy in ImageNet,  which is a dataset of over 14 million images belonging to 1000 classes. A
Read more