Supervised Learning(Part-4)

  Decision Trees

In the Machine Learning world, Decision Trees are a kind of non parametric models, that can be used for both classification and regression.

This means that Decision trees are flexible models that don’t increase their number of parameters as we add more features (if we build them correctly), and they can either output a categorical prediction (like if a plant is of a certain kind or not) or a numerical prediction (like the price of a house).

They are constructed using two kinds of elements: nodes and branches. At each node, one of the features of our data is evaluated in order to split the observations in the training process or to make an specific data point follow a certain path when making a prediction.

When they are being built decision trees are constructed by recursively evaluating different features and using at each node the feature that best splits the data. This will be explained in detail later.

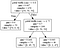
Probably the best way to start the explanation is by seen what a decision tree looks like, to build a quick intuition of how they can be used. The following figure shows the general structure of one of these trees.

In this figure we can observe three kinds of nodes:

• The Root Node: Is the node that starts the graph. In a normal decision tree it evaluates the variable that best splits the data.
• Intermediate nodes: These are nodes where variables are evaluated but which are not the final nodes where predictions are made.
• Leave nodes: These are the final nodes of the tree, where the predictions of a category or a numerical value are made.

Training process of a Decision Tree

Like we mentioned previously, decision trees are built by recursively splitting our training samples using the features from the data that work best for the specific task. This is done by evaluating certain metrics, like the Gini index or the Entropy for categorical decision trees, or the Residual or Mean Squared Error for regression trees.

The process is also different if the feature that we are evaluating at the node is discrete or continuous. 

• For discrete features all of its possible values are evaluated, resulting in N calculated metrics for each of the variables, being N the number of possible value for each categorical value. 
• For continuous features the mean of each two consecutive values (ordered from lowest to highest) of the training data are used as possible thresholds.

The result of this process is, for a certain node, a list of variables, each with different thresholds, and a calculated metric (Gini or MSE) for each variable/threshold tandem. Then, we pick the variable/threshold combination that gives us the highest/lowest value for the specific metric that we are using for the resulting children nodes (the highest reduction or increase in the metric).

Gini for categorical trees and Mean Squared Error for regression trees

Let's see an example of two decision trees, a categorical one and a regressive one to get a more clear picture of this process. The following figure shows a categorical tree built for the famous Iris Dataset, where we try to predict a category out of three different flowers, using features like the petal width, length, sepal length, …

Decision tree built for the Iris Dataset

We can see that the root node starts with 50 samples of each of the three classes, and a Gini Index (as it is a categorical tree the lower the Gini Index the better) of 0,667.

In this node, the feature that best split the different classes of the data is the petal width in cm, using as a threshold a value of 0,8. This results in two nodes, one with Gini 0 (perfectly pure node that only has one of the types of flowers) and one with Gini of 0.5, where the two other kinds of flowers are grouped.

In this intermediate node (False path from the root node), the same feature is evaluated (yes, this can happen, and it actually happens often if the feature is important) using a threshold of 1,75. Now this results in two other children nodes that are not pure, but that have a pretty low Gini Index.

In all of these nodes all the other features of the data (sepal length, sepal width, and petal length) were evaluated, and had their resulting Gini Index calculated, however, the feature that gave us the best results (lowest Gini Index) was the petal width.

The reason the tree didn’t continue growing is because Decision Trees always a growth-stop condition configured, otherwise they would grow until each training sample was separated into its own leave node. These stop conditions are maximum depth of the tree, minimum samples in leave nodes, or minimum reduction in the error metric.